関数電卓が沢山になった。でも使う機会はあまりない。学生時代はちょくちょく使ったけど今は普通の電卓で十分な計算ばかり、たまーに10進→16進→2進数の基数変換に使う程度。。これだけあると、ポチポチ押して楽しむだけではちょっと可愛そう。
なにか実用的(そうな)計算をしてみたいですね。いや学生時代は電気系だったのでそれ系をすればいいじゃんってところですが、そんなのすっかり忘れています。あ、1/(2π√(LC))は覚えていますね、共振周波数。
でもまあちょっと初級編あたりから、なんか実用で使われていそうな計算をやってみようかなと思ったわけです。
ボール投げシミュレーション計算
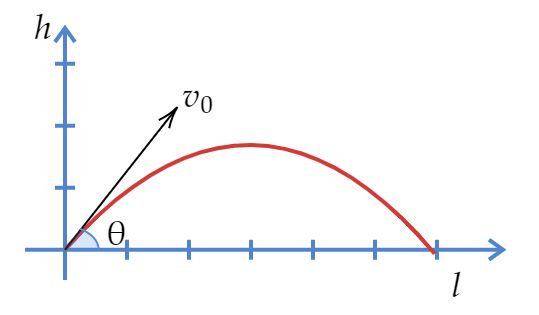
そこでボール投げシミュレーション!
ボールを上に向かって投げ上げて重力で地面に落ちるまでの距離などの式ですね。
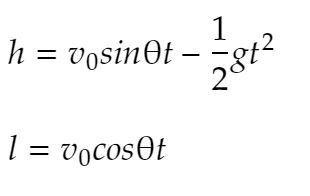
こんなやつです。
よくこの式でv0が与えられますが、スピードガンでもなければそんなものは無い。
ボール投げをして、どの角度で投げたら何メートル飛んだか。この値から初速を調べる。
という計算をしてみます。
上の式の1つめを時間tでくくると
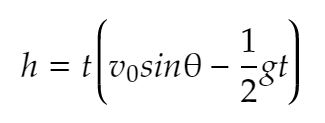
ですね、どれだけ飛んだかは初速と角度、時間で決まりますが、h=0の時に着地しますので、h=0の時の方程式を解けばよいわけですね。この方程式だとt=0のときもh=0になりますが、これは初期値なのでもう一つの方
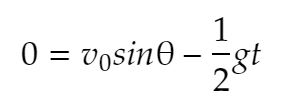
これを解けば良いのですね。ですが着弾までの時間はわからないので、tを消去します。

これをtに代入します
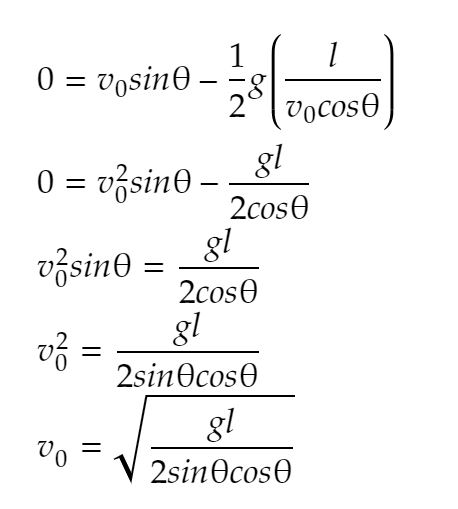
ほうほう、ボール投げで投げた角度と何メートル飛んだかで初速がわかるわけですね。
gは重力加速度の9.8です。
次の計算
v0が求まると、あとはこの初速のまま45度で投げたら何m飛んだのか?とか考えられるわけです。ボール投げで45度の角度で投げれば効率が良いのはわかっていますが、では実際何メートル伸びるのか?関数電卓でプログラムを組んでボール投げトレーニングに使えるというわけです。
まあ実際にははじめの高さは肩の高さだとか空気抵抗だとか色々あるのでしょうが、電卓で何か実用的っ「ぽい」ことができれば良いのです。
v0が判ってその同じ力で角度θを変えて投げた時の飛距離を計算してみると
上の途中の式をlの式に変換して、θは新θを入れる。
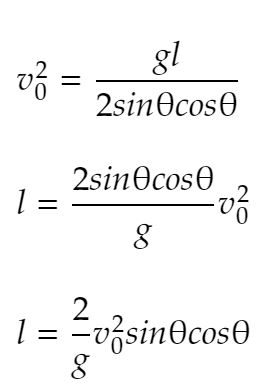
gは定数ですね。
というわけで電卓のプログラムに入れるわけです。
? → A:? → B:√(4.9×A÷sinB÷cosB) → C▲? → D: 2÷9.8×C^2×sinD×cosD Min▲
A:ボール投げの飛距離
B:ボール投げあげ角度
C:AとBで求めた初速
D:Cの初速・Dの角度で投げたときの飛距離
飛距離・角度を入れたあと、初速が計算されて表示、シミュレーション角度を入れてその時の飛距離を計算します。
でも、こうするとシミュレーション角度に0が入ったら終了で、この角度だったら?を繰り返しシミュレーションできるような連続シミュレーションも可能になります
? → A:? → B:√(4.9×A÷sinB÷cosB) → C▲Lbl 0:? → D: D = 0 ⇒ Goto 1 : 2÷9.8×C^2×sinD×cosD Min▲Goto 0:Lbl 1 :M
実行すると、飛距離20m・30度で投げた場合、15.044m/sの速さで投げたことになります。
これを45度で投げた場合、23.1mになります。30度で投げた場合、…それは20mですね。
なんか使えそう?
これは過去のfx-3650Pの紹介の時にやったやつですね。今回はfx-700AZに入れてやってみました。
いや、結果は同じですけどね(笑)
sinとかcosとか使っていると関数電卓使っている感がしますね。

